Explanation

어느 모형을 선택하느냐에 따라 하이퍼플레인이 달라진다. NN과 Decision tree의 경우 아웃라이어에 취약한 성질이 있다. 이 때 앙상블 모형은 여러 가지 모델을 합치는 것이라고 생각하면 된다. 모형의 Bias와 Variance에서 앙상블 모형은 주로 Variance를 낮추는 방향으로 작동한다.(물론 Bias를 낮추면서 작용하는 경우도 있다.) 대부분의 머신러닝 기법들은 테스트 데이터셋에 대해 low bias and high variance의 over-fitting 양상을 띈다. 이 경우에는 Variance를 낮추는 것이 목표이고 앙상블 모형, 특히 Bagging이 해당 케이스에 사용된다. Unstable Classifiers : DT and NN / Stable Classifiers : Logistic rgl, LDA Instability자체가 앙상블 모형에서는 필수이다.

Bagging

Bootstrapping은 복원추출을 여러번 하는 것(주로 100번 이상)을 의미한다. 그렇기 때문에 데이터에서 같은게 2번 이상 뽑힐수도, 아예 안 뽑힐 수도 있다. 이 경으 각 데이터셋에 따라 모델을 구축하고, 해당 모델의 Predicted class label을 계산한다. 모델의 구매확률 예측값에 평균을 내거나 예측 라벨에 다수결 투표를 진행하여 최종 결과값을 구한다. Bagging은 Bootstrapping Aggregating을 말하며, 복원추출된 데이터셋에 대한 의사결정나무의 예측 결과를 취합하여 생성한다. 해석력은 잃어버리지만 예측력은 높아지는 모형이다.

Bagging process

트리 갯수에 따라 분류 경계면은 변화한다. 그리고 트리의 갯수가 많아질수록 분류경계면은 촘촘한 계단 형태를 띈다.(Super resolution system과 관련이 있는건가?) 트리 갯수가 커지면 분류경계면은 다양한 형태를 보일 수 있다.

\[ T^1, ..., T^B \] \[ C(x,T^1), ..., C(x,T^B) \] \[ N_j = \sum_{b=1}^B I[C(x,T^b)=j] , j = 1, ..., J\] \[ C_B(x) = argmax_j N_J \] B개의 Training data가 있으며 C는 각각 트리 하나라고 보면 된다.(주로 트리를 이용하지만 다른 모델일 수도 있다.) 그리고 \(N_j\)는 투표수를 의미하며 트리 예측결과와 실제 결과값 j를 비교한다. 그 후 다수결로 마무리 하는 것이다. 이런 프로세스는 전문가 위원회에서 투표로 무엇인가를 결정하는 것과 유사하다.

Goal

결국 앙상블의 목표는 오류를 줄이는 것이다. 분산감소에 집중하는 형태는 Bagging, Random Forest가 있고 편향감소에 집중하는 형태로는 Boosting이 있다. 그리고 목표달성을 위해 앙상블의 필수 아이디어는 ’결국 다양성을 어떻게 확보할 것인가?’이다.

german = read.table("germandata.txt", header=T)
german$numcredits = factor(german$numcredits)
german$residence = factor(german$residence)
german$residpeople = factor(german$residpeople)

library(rpart)
library(adabag)
## 필요한 패키지를 로딩중입니다: caret
## 필요한 패키지를 로딩중입니다: lattice
## 필요한 패키지를 로딩중입니다: ggplot2
## 필요한 패키지를 로딩중입니다: foreach
## 필요한 패키지를 로딩중입니다: doParallel
## 필요한 패키지를 로딩중입니다: iterators
## 필요한 패키지를 로딩중입니다: parallel
library(pROC)
## Type 'citation("pROC")' for a citation.
## 
## 다음의 패키지를 부착합니다: 'pROC'
## The following objects are masked from 'package:stats':
## 
##     cov, smooth, var
set.seed(1234)
i = sample(1:nrow(german), round(nrow(german)*0.7))
german.train = german[i,]
german.test = german[i,]
my.control <- rpart.control(xval=0, cp=0, minsplit=5, maxdepth=10)
bag.train.german <- bagging(y~., data=german.train, mfinal=50, control=my.control)
importanceplot(bag.train.german)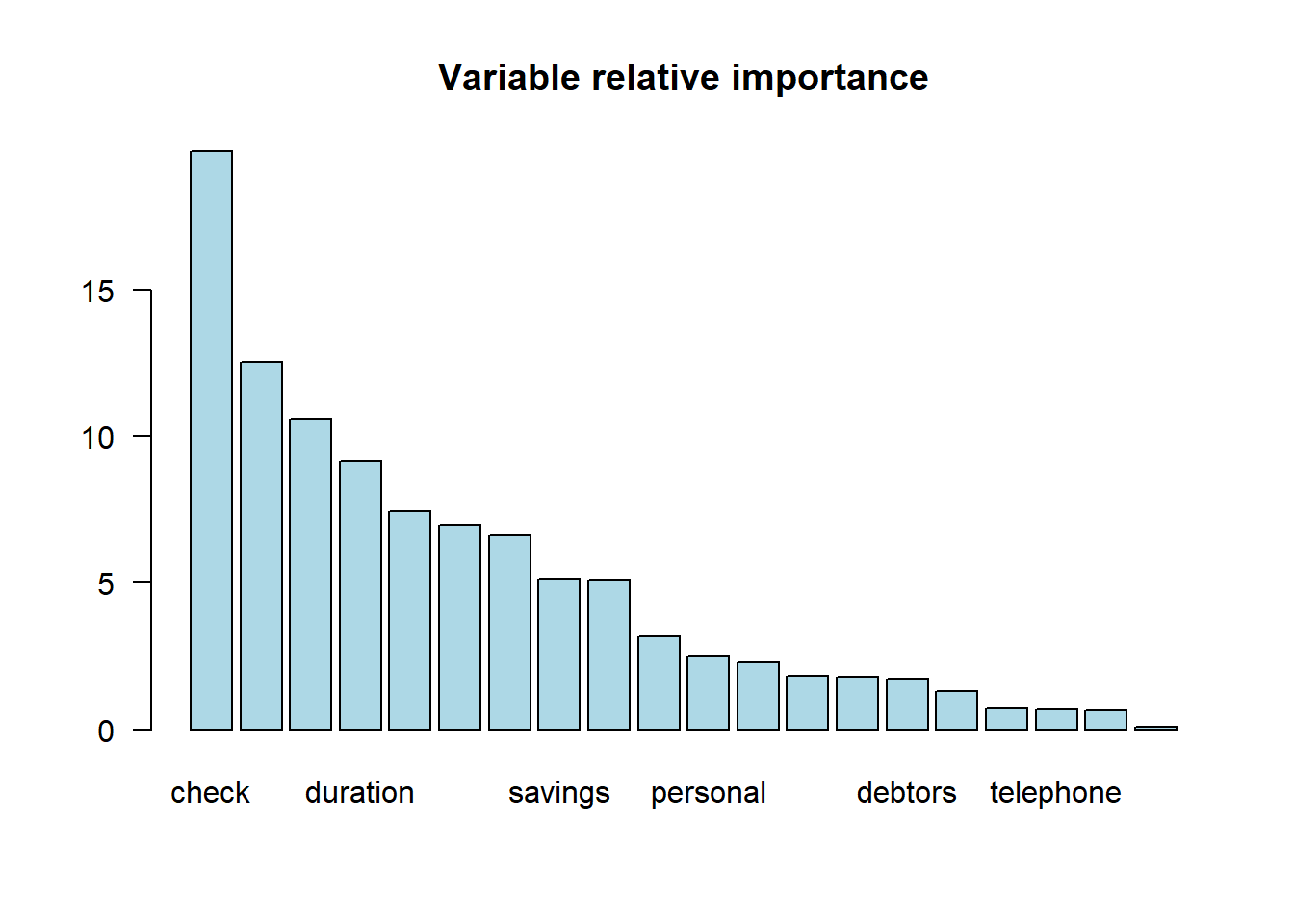

pred.bag.german <- predict.bagging(bag.train.german, newdata=german.test)
print(pred.bag.german$confusion)
##                Observed Class
## Predicted Class bad good
##            bad  191    0
##            good  18  491

head(pred.bag.german$prob)
##      [,1] [,2]
## [1,] 0.00 1.00
## [2,] 0.02 0.98
## [3,] 0.84 0.16
## [4,] 0.00 1.00
## [5,] 0.64 0.36
## [6,] 0.00 1.00
rocbag <- roc(german.test$y ~ pred.bag.german$prob[,1])
## Setting levels: control = bad, case = good
## Setting direction: controls > cases
plot(rocbag)

auc(rocbag)
## Area under the curve: 0.9992
a <- data.frame(matrix(c(1,2)))
colnames(a) <- '가.가'
a$가.가
## [1] 1 2

Boosting

Bagging은 데이터를 바꾸고 가중치를 그대로 사용했다면 Boosting은 데이터는 그대로지만 가중치를 바꾼다. 주로 경계선 근처의 데이터들이 오분류 확률이 높기 때문에 해당 데이터들에게 높은 가중치를 부여한다. AdaBoost와 Gradient Boost(+XGB)를 주로 이용한다. 예측하기 어려운 것들에 웨이트를 부여하여 편향을 줄이겠다는 아이디어이다. 이 때 재밌는 것은 배깅에서는 큰 사이즈의 트리를 사용하고 부스닝에서는 작은 사이즈의 트리를 사용하는 것이 좋다.

my.control <- rpart.control(xval=0, cp=0, maxdepth=1)
boo.train.german <- boosting(y~., data=german.train, boos=T, mfinal=100, control=my.control)
pred.boo.german <- predict.boosting(boo.train.german, newdata=german.test)
rocboost <- roc(german.test$y ~ pred.boo.german$prob[,1])
## Setting levels: control = bad, case = good
## Setting direction: controls > cases
plot(rocboost)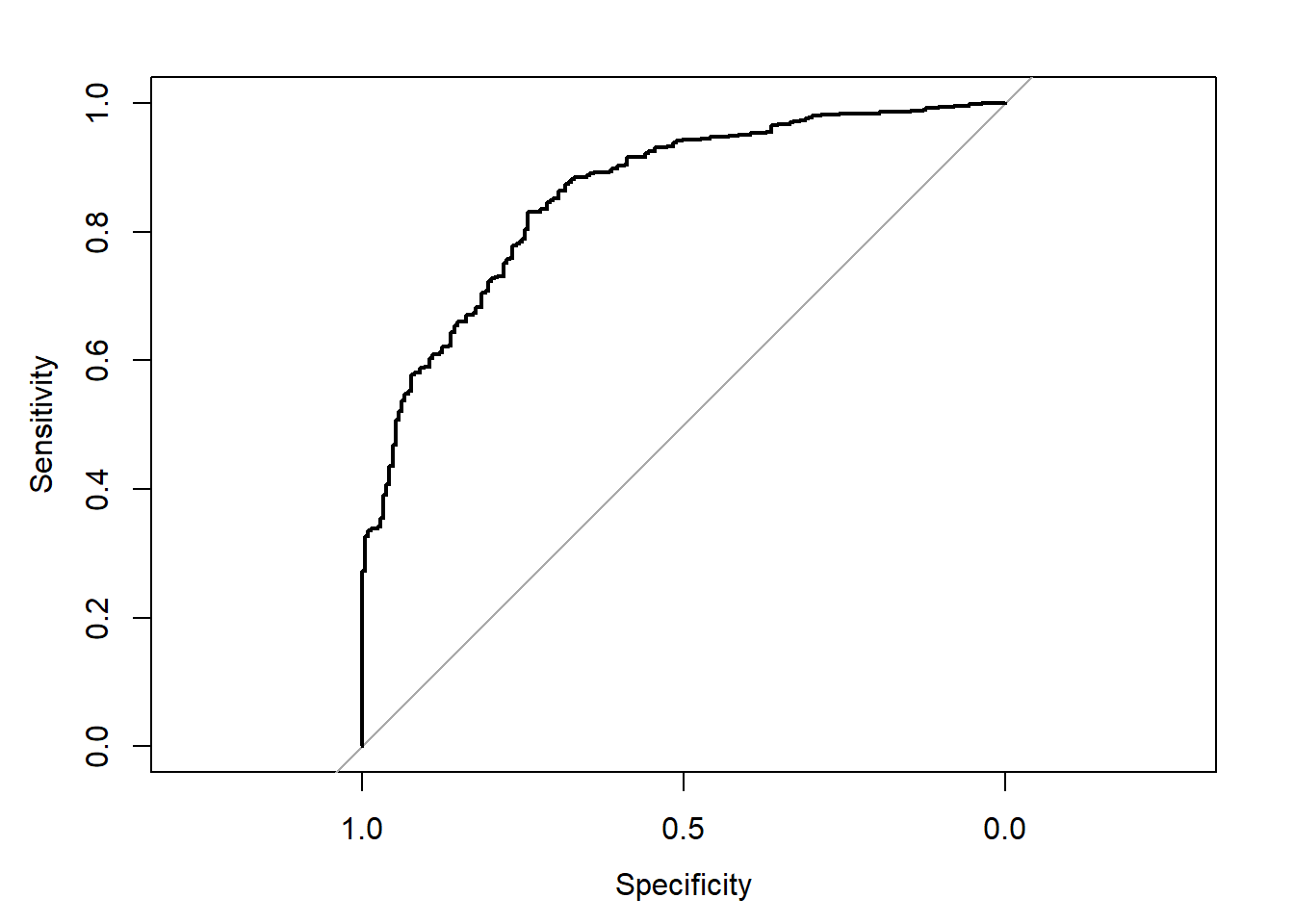

Adaboost, Gradient boost

Adaboost : Train a classifier f1 on D, then train a f2 to correct the errors of f1, then f3 to correct the errors of f2, etc. Gradient boost : 이전의 트리를 계속 더해주면서 에러텀을 추가해주는 모델이다.

Random Forest

의사결정나무를 이용한 배깅의 특수한 형태를 취하는 앙상블 기법이다. Bootstrapping + 변수임의추출을 통하여 다양성을 확보한다. Bagging을 하게 되면 중요도 높은 변수가 자주 발생하므로, 랜포에서는 중요한 변수가 덜 나오도록 X변수를 임의추출한다. 트리들을 독립으로 만들기 위해 추출을 하는 것이며 노드 분할 시 p개 변수 중 m개의 변수 중 탐색하여 분할한다. m이 너무 작은 경우에는 트리간 상관관계는 감소하지만 정확도가 떨어진다. 일반적으로 \(m = \sqrt{p}\)를 이용한다. 결과를 종합하는 방식에서 다수결 투표를 할수도 있고 가중치 투표를 할 수도 있다. Training Accuracy로 부여한다. 혹은 그냥 예측값의 평균을 이용하기도 한다.

Variable importance

랜덤포레스트에서 변수중요도 계산시 OOB(Out of bag error)를 이용한다. 학습 데이터셋에서 선택받지 않은 데이터들을 검증용으로 사용하는 방식이다. 먼저 전체 OOB Error를 구하고 그 다음에 각 변수를 하나씩 하나씩 섞으면서 각 변수에 대한 에러를 구한다. 그 때 변수를 섞지 않았을 때보다 섞었을 때 에러가 더 높으면 해당 변수가 중요하다고 판단이 된다.