Unsupervised Learning-Clustering
Jun 15, 2020 21:13 · 794 words · 4 minute read
Intro
2020-1학기 김현중 교수님의 데이터마이닝 수업.
Explanation
Unsupervised learning은 타겟변수가 따로 정해져 있지 않다. 그렇기 때문에 마케팅에서 고객 세분화에 주로 이용이 된다. 군집화는 유사성보다 비유사성을 기준으로 하며 거리를 이용한다. 또한 주로 연속형 변수에 대해 사용되며 범주형의 경우에는 범주별 거리의 의미파악이 힘들기 때문에 잘 사용하지 않는다.(사용하더라도 지시변수로 바꿔서 이용하지만 훌륭한 분석은 아니다.)
Distance Measures
가장 대표적인 방식으로 Euclidean 방식이 있다. \[ \begin{array} d(x,y) = (\sum_{i=1}^p (x_i - y_i)^2)^\frac{1}{2} \end{array} \]
Minkowski 거리 \[ d(x,y) = (\sum_{i=1}^p (x_i - y_i)^m)^\frac{1}{m} \] Mahalanobis 거리 \[ d(x,y) = \sqrt{(x-y)^{'}S^{-1}(x-y)} \]
Mahalanobis 거리의 경우에는 점들의 분산을 고려하기 때문에 좋은 방식이다. 다른 거리들은 분산을 고려하지 않으므로 변수간 독립을 가정한다고 생각하면 된다. 여기서 \(S^(-1)\)는 공분산 행렬의 의미를 지닌다. 그렇지만 차원이 높은 경우 역행렬 계산이 힘든 단점이 있다.
Manhattan Distance \[ d_{Manhattan(X,Y)} = \sum_{i=1}^p |x_i - y_i| \]
해당 거리는 지도에서의 거리이며 직선거리가 아니라 실제거리(직각)를 나타내는데 유용하다.
Standardization
거리에 자료의 단위가 큰 영향을 미치기에, 표준화는 필수이다. 주로 평균0, 표준편차1을 만들어준다. 관측치 표준화와 변수 표준화 두개로 나뉘는데, 관측치 표준화의 예시로는 단위면적당 판매량이나 인구 10만명당 범죄수가 있다. 변수 표준화는 feature scaling을 의미한다.
Hierarchical Clustering
Distance matrix를 만드는 것이 생명이다. 이 때 군집의 수는 사용자가 임의로 설정해야한다. 군집의 수 N에 대해 N by N matrix D는 군집간 거리를 그 원소로 가진다. 이 때 D는 단계별로 행렬 사이즈가 줄어드는데, 가장 가까운 관계에 있는 두 군집을 하나의 행과 열로 합치면서 행렬의 크기가 작아진다. 따라서 이 프로세스를 Dendrogram으로 표현할 수 있다.
거리를 계산하는 기준은 크게 5가지가 있다. Single Linkage, Complete Linkage, Average Linakge, Centroid Method, Ward’s Method.
data("USArrests")
zUSArrests=scale(USArrests)
summary(zUSArrests)
## Murder Assault UrbanPop Rape
## Min. :-1.6044 Min. :-1.5090 Min. :-2.31714 Min. :-1.4874
## 1st Qu.:-0.8525 1st Qu.:-0.7411 1st Qu.:-0.76271 1st Qu.:-0.6574
## Median :-0.1235 Median :-0.1411 Median : 0.03178 Median :-0.1209
## Mean : 0.0000 Mean : 0.0000 Mean : 0.00000 Mean : 0.0000
## 3rd Qu.: 0.7949 3rd Qu.: 0.9388 3rd Qu.: 0.84354 3rd Qu.: 0.5277
## Max. : 2.2069 Max. : 1.9948 Max. : 1.75892 Max. : 2.6444
hc1 = hclust(dist(zUSArrests),method="average")
plot(hc1, hang = -1)
rect.hclust(hc1, k=5)
cluster <- cutree(hc1, k=5) #모델자체가 들어가야한다.
cent <- NULL
for(k in 1:5){
cent <- rbind(cent, colMeans(USArrests[cluster == k,]))
}
cent
## Murder Assault UrbanPop Rape
## [1,] 14.671429 251.28571 54.28571 21.685714
## [2,] 10.000000 263.00000 48.00000 44.500000
## [3,] 10.883333 256.91667 78.33333 32.250000
## [4,] 5.530435 129.43478 68.91304 17.786957
## [5,] 2.700000 65.14286 46.28571 9.885714계층적 군집분석 장단점
군집의 수를 알 필요가 없으며 덴드로그램을 통한 시각화가 가능한 것이 장점이다. 하지만 계산속도가 느리다.
K-means Clustering
사전에 결정된 군집수 k에 기초한 클러스터링이다. EM Algorithm과 연결이 된다. Initialization 후 군집 내 평균찾는 것을 값이 수렴하거나 일정 수 이상의 iteration이 나올 때 까지 반복. 신속하게 계산이 가능하지만 초기 군집수 K를 결정하기 어려우며 군집결과의 해석이 용이하지 않을 수 있다.
K는 어떻게 결정해야하는가?
사후판단의 방식으로 Elbow point 혹은 Silhouette plot을 이용한다. PCA와 같은 차원 축소로 시각화를 하여 K를 결정할 수도 있고 혹은 하이브리드 방식으로 대용량 데이터를 sampling하여 계층정 군집분석을 통한 Dendogram 시각화로 결정할 수도 있다.
set.seed(1234)
kmc1 = kmeans(zUSArrests,4)
kmc1
## K-means clustering with 4 clusters of sizes 13, 13, 8, 16
##
## Cluster means:
## Murder Assault UrbanPop Rape
## 1 0.6950701 1.0394414 0.7226370 1.27693964
## 2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
## 3 1.4118898 0.8743346 -0.8145211 0.01927104
## 4 -0.4894375 -0.3826001 0.5758298 -0.26165379
##
## Clustering vector:
## Alabama Alaska Arizona Arkansas California
## 3 1 1 3 1
## Colorado Connecticut Delaware Florida Georgia
## 1 4 4 1 3
## Hawaii Idaho Illinois Indiana Iowa
## 4 2 1 4 2
## Kansas Kentucky Louisiana Maine Maryland
## 4 2 3 2 1
## Massachusetts Michigan Minnesota Mississippi Missouri
## 4 1 2 3 1
## Montana Nebraska Nevada New Hampshire New Jersey
## 2 2 1 2 4
## New Mexico New York North Carolina North Dakota Ohio
## 1 1 3 2 4
## Oklahoma Oregon Pennsylvania Rhode Island South Carolina
## 4 4 4 4 3
## South Dakota Tennessee Texas Utah Vermont
## 2 3 1 4 2
## Virginia Washington West Virginia Wisconsin Wyoming
## 4 4 2 2 4
##
## Within cluster sum of squares by cluster:
## [1] 19.922437 11.952463 8.316061 16.212213
## (between_SS / total_SS = 71.2 %)
##
## Available components:
##
## [1] "cluster" "centers" "totss" "withinss" "tot.withinss"
## [6] "betweenss" "size" "iter" "ifault"
pairs(zUSArrests, col=kmc1$cluster, pch=16)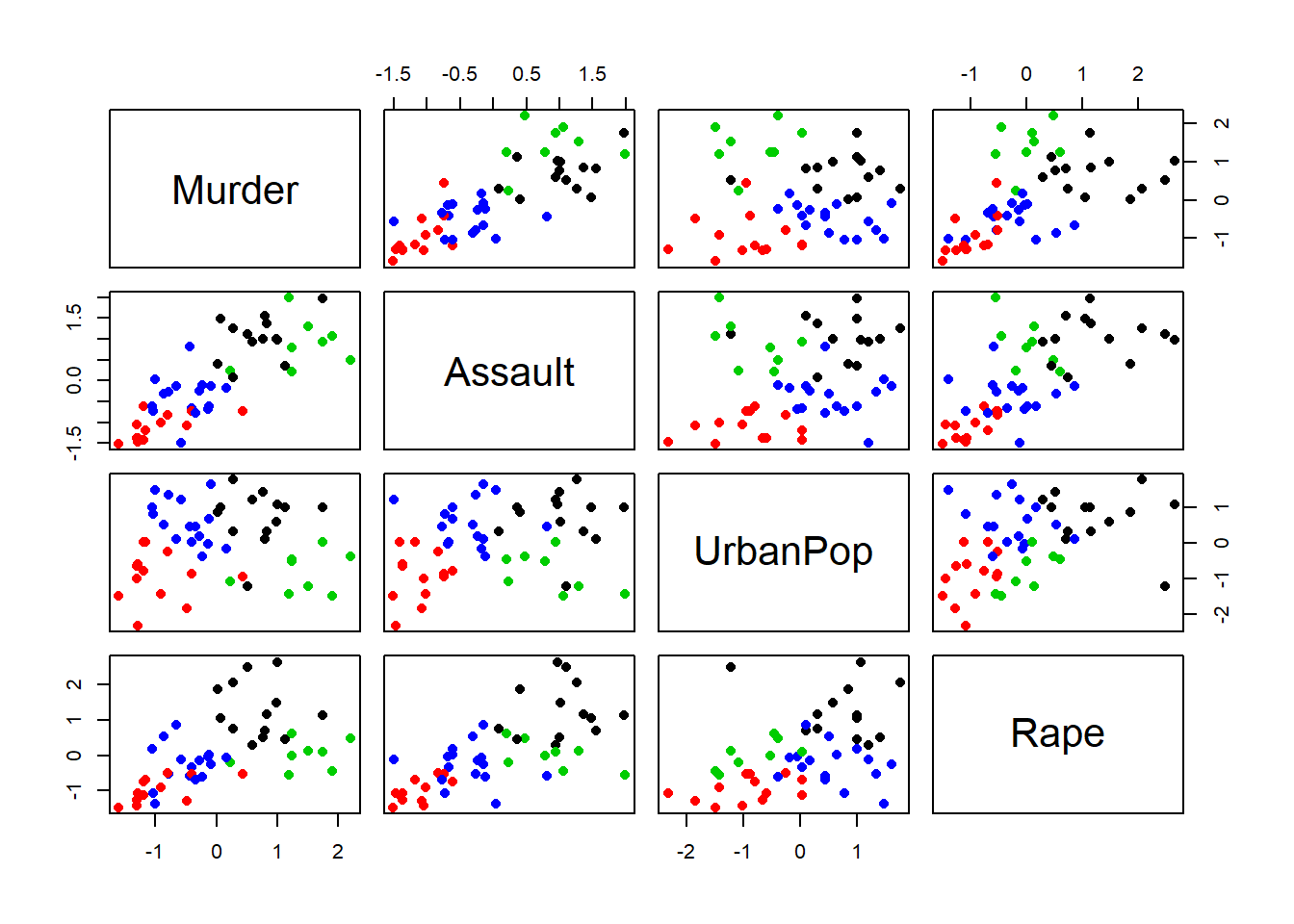
#Elbow point
wss = 0
for (i in 1:10) {
wss[i] = sum(kmeans(zUSArrests, center=i)$withinss)
}
plot(1:10, wss, type='b', xlab="Number of Clusters", ylab="Within group sum of squares")
# Wss는 군집중심과 군집내 관찰값간의 거리제곱합을 의미
# wss는 데이터의 분산을 나타낸다.K-medoid Clustering
조금 더 로버스트한 모형을 만들기 위하여, 군집 내 대표값을 평균이 아니라 중앙값으로 설정하는 방식이다.
Silhouette
실루엣 값은 각 데이터포인트별로 값이 나온다. i번째 데이터에 대해서 해당 데이터의 군집 내 개체들간의 거리, 그리고 타군집 개체들과의 거리를 계산하여 값을 도출한다.
Densely-based Clustering
데이터의 거리뿐만 아니라, 분산도 고려하는 방식이다. dbscan을 이용하며 Eps(반지름)를 파라미터로 결정해야 한다.