library(MASS)
wais <- read.csv('WAIS-data-Table22-12.csv')[,-2]
head(wais)
##   IGROUP INFORMATION SIMILARITIES ARITHMETIC PICTURE
## 1      2           9            5         10       8
## 2      2          10            0          6       2
## 3      2           8            9         11       1
## 4      2          13            7         14       9
## 5      2           4            0          4       0
## 6      2           4            0          6       0

Data description

WAIS Data: Wechsler Adult Intelligence Scale for two categories of people
group1: people who do not present a senile factor(노인성 인자)
group2: people who do present a senile factor

변수명	데이터 타입	변수 설명
X1	NUM	Information
X2	NUM	Similarities
X3	NUM	Arithmetic
X4	NUM	Picture completion

group1은 노인성 인자를 보이지 않는 그룹이고 group2는 노인성 인자를 보인은 그룹이다. 현재 WAIS에 따라 각 피험자에 대한 4가지 지표로 표현된 데이터를 구하였다. 이 때, 이 4가지 지표(X1,⋯,X4)를 기준으로 IGROUP 1,2가 나뉘었을 때 이 분류를 가장 잘 나타내는 선은 무엇일까? 현재 독립변수를 INFORMATION, SIMILIARITIES, ARITHMETIC, PICTURE로 잡고 종속변수를 IGROUP으로 판단할 수 있다. 그리고 이 상황에서 LDA(Linear Discriminant Analysis)를 통하여 regrouping 후 실제 분류값과 비교할 것이다. LDA는 그룹내분산의 최소화, 그룹간거리의 최대화를 기준으로 선을 긋는다. 그룹이 2개로 나누어져있으므로 판별기준은 선으로 나타난다.

Analysis

현재 데이터를 이용해 알 수 있는 sample prior probability는 3749(group1), 1249(group2)이다. 그리고 실제 LDA를 한 결과는 다음과 같다.

(ld.wais <- lda(formula = IGROUP~. , data=wais))
## Call:
## lda(IGROUP ~ ., data = wais)
## 
## Prior probabilities of groups:
##        1        2 
## 0.755102 0.244898 
## 
## Group means:
##   INFORMATION SIMILARITIES ARITHMETIC  PICTURE
## 1    12.56757     9.567568   11.48649 7.972973
## 2     8.75000     5.333333    8.50000 4.750000
## 
## Coefficients of linear discriminants:
##                       LD1
## INFORMATION  -0.016892707
## SIMILARITIES -0.132789096
## ARITHMETIC   -0.005504696
## PICTURE      -0.285326128
apply(ld.wais$means %*% ld.wais$scaling, 2, mean)
##       LD1 
## -3.039502

계수는 다음과 같이 나타난다.
-0.017(INFO), -0.133(SIM), -0.006(ARTH), -0.285(PICT)

계수는 lda로 계산된 식의 계수를 의미하며. 여기서는 1,2로 두개의 범주가 나눠져있으므로 ld1만 나타난다. apply를 통해 계산한 값은 판별함수의 상수항이며 계수에 평균값을 실제 대입하면 얻을 수 있는 값이다.

library(tibble)
REGROUP = predict(ld.wais, wais)$class
wais <- add_column(wais, REGROUP, .after='IGROUP')
wais$IGROUP <- as.factor(wais$IGROUP)
head(wais)
##   IGROUP REGROUP INFORMATION SIMILARITIES ARITHMETIC PICTURE
## 1      2       1           9            5         10       8
## 2      2       2          10            0          6       2
## 3      2       2           8            9         11       1
## 4      2       1          13            7         14       9
## 5      2       2           4            0          4       0
## 6      2       2           4            0          6       0

wais의 데이터를 실제 LDA를 통해 regrouping한 결과를 열에 추가하였다. 그렇다면 실제 IGROUP과 REGROUP은 얼마만큼의 차이가 있을까?

library(GGally)
## 필요한 패키지를 로딩중입니다: ggplot2
## Registered S3 method overwritten by 'GGally':
##   method from   
##   +.gg   ggplot2
ggpairs(wais[,-2], aes(colour=IGROUP))
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

ggpairs(wais[,-1], aes(colour=REGROUP))
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.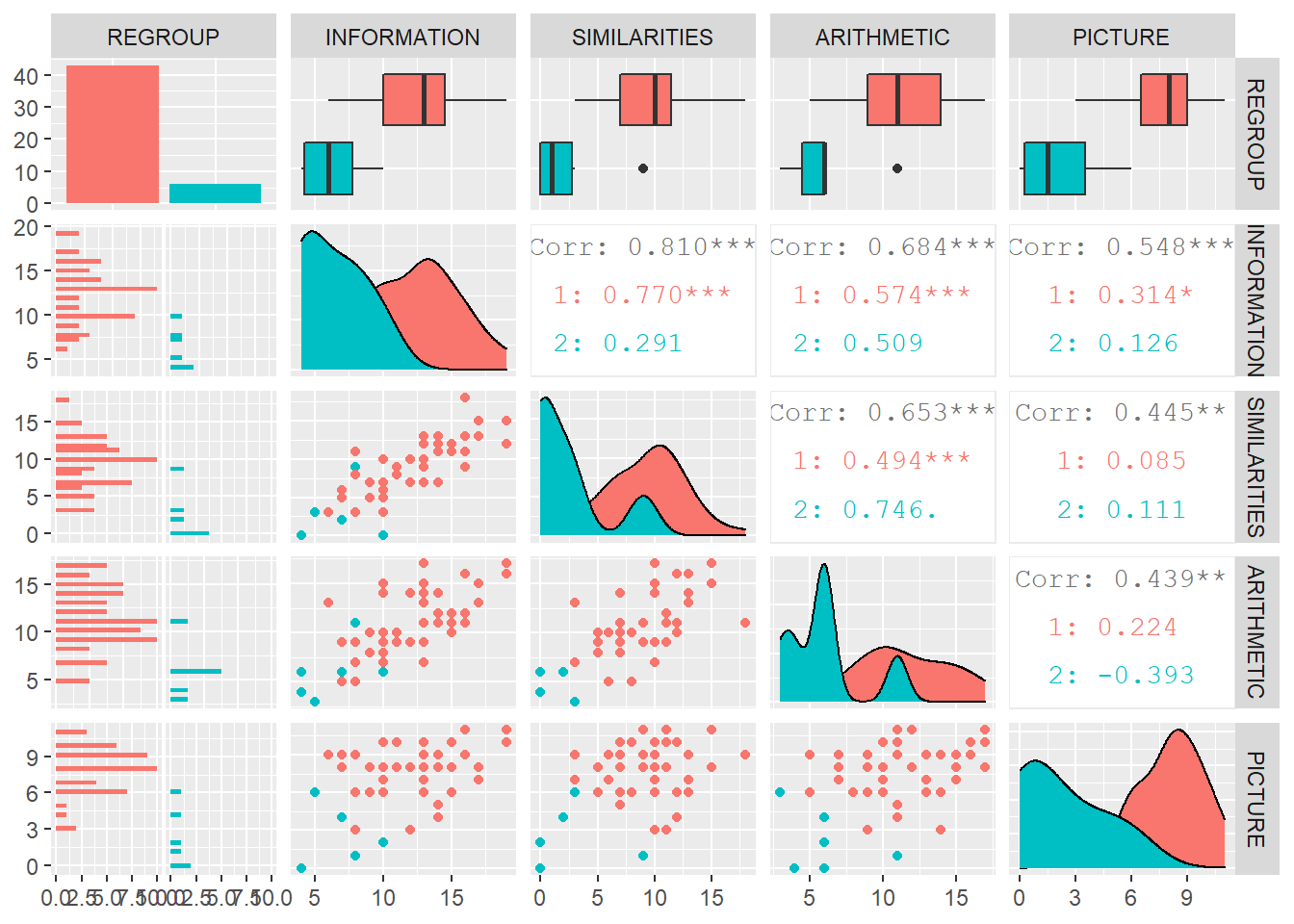

table(wais[,1], wais[,2])
##    
##      1  2
##   1 37  0
##   2  6  6

위의 플랏은 IGROUP을 기준으로 색이 나뉜 것이고, 밑의 플랏은 REGROUP을 기준으로 색을 나눈 것이다.
테이블에서 보이듯이 정분류는 43개이며, 오분류는 6개이다. 정분류는 1을 1로 분류한 것이 36개, 2를 2로 분류한 게 6개이다. 그리고 igroup의 2를 regroup에서 1로 오분류 한것이 6개로 나타난다. 오분류의 확률은 649로 나타난다.

plot(ld.wais)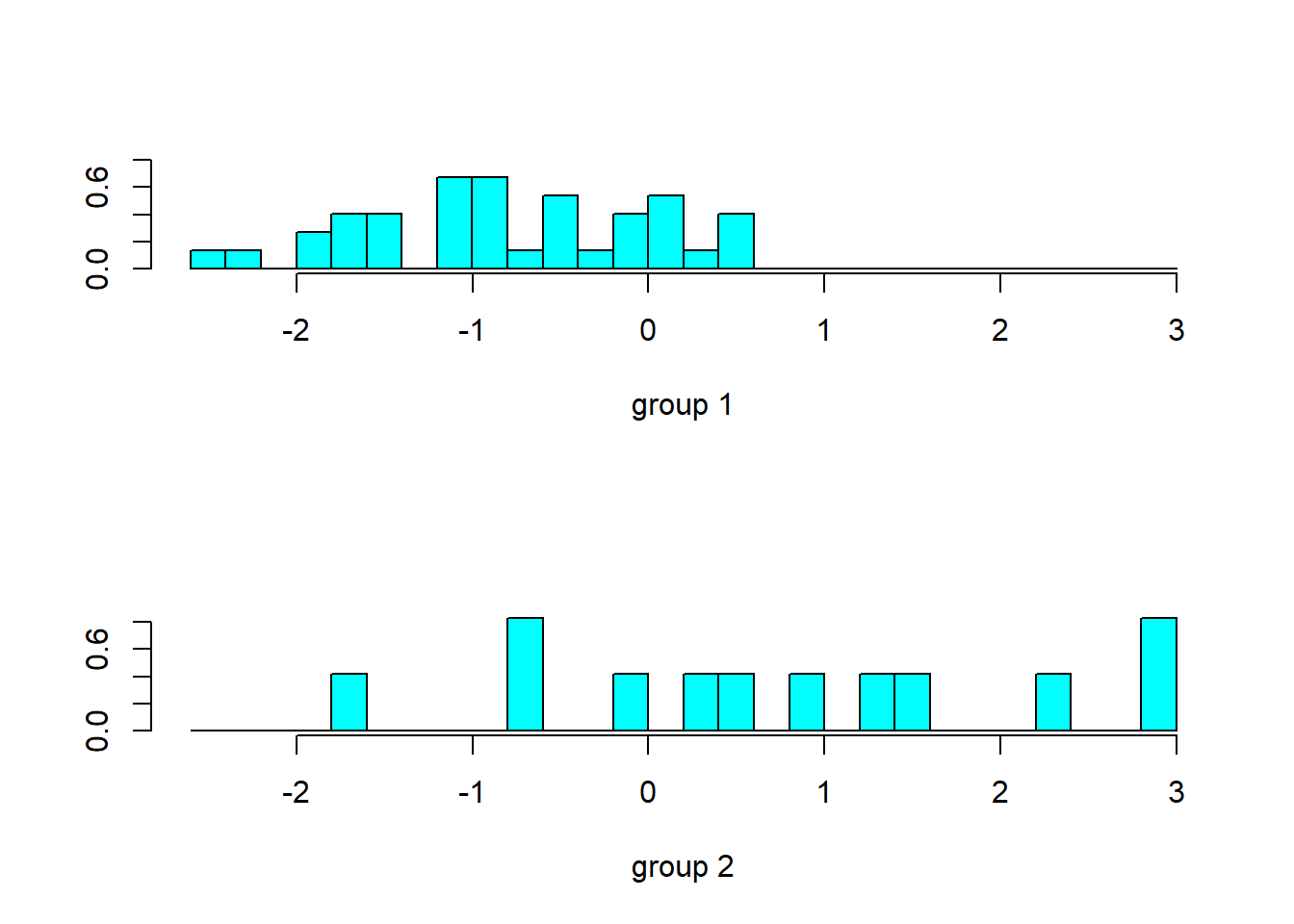

위의 그래프는 각 그룹의 데이터가 new axis에 projection된 후의 분포를 나타낸다. 실제 group1과 group2는 new axis의 0을 기준으로 어느정도 판별이 되고 있음을 보인다.